Creating a Koch Snowflake
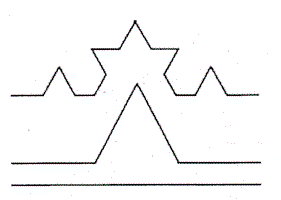Consider the straight line segment at the bottom of the figure to the left, and assume that it has unity length. Implement a first iteration of this line by dividing it in thirds, and then replacing the middle segment by the two legs, each of length 1/3, as shown in the middle figure. The path length of this first iteration is 4/3. Now move on to Iteration 2, applying the same procedure to each of the four line segments of Iteration 1. This yields the upper figure to the left whose path length is (4/3)2. It is clear that after N such iterations, the path length is (4/3)N. Applying this procedure for larger and larger values of N, it is clear that the path length has no upper bound.
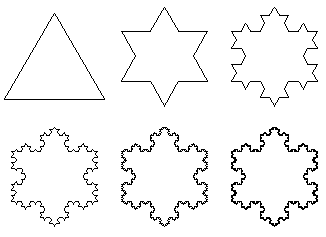The Koch Snowflake is born as an equalateral triangle, as shown in the figure to the right, with each of its sides then undergoing the procedure noted above, allowing N to increase without bound. The perimeter of the snowflake is clearly infinite. Its area is derived by summing the ever increasing number of ever smaller equalateral triangles. This results in a geometric series which identifies its area as 1.6 times the area of the initial triangle. The figures to the right display the results of the first five iterations.
This beautiful snowflake has been studied in great detail, and displays, along with its siblings, many more additional properties that are striking. Several websites provide a much greater depth of analysis. See, for example,
http://www.geom.umn.edu
http://www.ccs.neu.edu